6.1. Matrix multiply¶
This codes performs a matrix - matrix multiplication by means of a hybrid MPI/OmpSs implementation.
Note
You can dowload this code visiting the url http://pm.bsc.es OmpSs Examples and Exercises’s (code) link. This version of matrix multiply kernel is included inside the 04-mpi+ompss’s directory.
Groups of rows of the matrix A are distributed to the different MPI processes. Similarly for the matrix B, groups of columns are distributed to the different MPI process. In each iteration, each process performs the multiplication of the A rows by the B columns in order to compute a block of C. After the computation, each process exchanges with its neighbours the set of rows of A (sending the current ones to the process i+1 and receiving the ones for the next iteration from the process i-1).
An additional buffer rbuf is used to exchange the rows of matrix A between the different iterations.
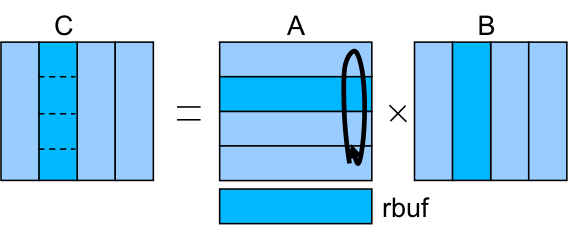
In this implementation of the code, two tasks are defined: one for the computation of the block of C and another for the communication. See the sample code snippet:
for( it = 0; it < nodes; it++ ) {
#pragma omp task // add in, out and inout
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans, n, n, m, 1.0, (double *)a, m, (double *)B, n, 1.0, (double *)&C[i][0], n);
if (it < nodes-1) {
#pragma omp task // add in, out and inout
MPI_Sendrecv( a, size, MPI_DOUBLE, down, tag, rbuf, size, MPI_DOUBLE, up, tag, MPI_COMM_WORLD, &stats );
}
i = (i+n)%m; //next C block circular
ptmp=a; a=rbuf; rbuf=ptmp; //swap pointers
}
The exercise is provided without the in, out and inout dependence clauses.
- Complete the pragmas in order to define the correct dependences
- Compile and run the example and check that the results are correct (the output of the computation already checks the correctness)
- Generate the tracefile and task graph of the execution