2. Programming model¶

2.1. Execution model¶

The OmpSs runtime system creates a team of threads when starting the user program execution. This team of threads is called the initial team, and it is composed by a single master thread and several additional workers threads. The number of threads that forms the team depend on the number of workers the user have asked for. So, if the user have required 4 workers then one single master thread is created and three additional workers threads will be attached to that initial team.

The master thread, also called the initial thread, executes sequentially the user program in the context of an implicit task region called the initial task (surrounding the whole program). Meanwhile, all the other additional worker threads will wait until concurrent tasks were available to be executed.

Multiple threads execute tasks defined implicitly or explicitly by OmpSs directives. The OmpSs programming model is intended to support programs that will execute correctly both as parallel and as sequential programs (if the OmpSs language is ignored).

When any thread encounters a loop construct, the iteration space which belongs to the loop inside the construct is divided in different chunks according with the given schedule policy. Each chunk becomes a separate task. The members of the team will cooperate, as far as they can, in order to execute these tasks. There is a default taskwait at the end of each loop construct unless the nowait clause is present.

When any thread encounters a task construct, a new explicit task is generated. Execution of explicitly generated tasks is assigned to one of the threads in the initial team, subject to the thread’s availability to execute work. Thus, execution of the new task could be immediate, or deferred until later according to task scheduling constraints and thread availability. Threads are allowed to suspend the current task region at a task scheduling point in order to execute a different task. If the suspended task region is for a tied task, the initially assigned thread later resumes execution of the suspended task region. If the suspended task region is for an untied task, then any thread may resume its execution.

The OmpSs specification makes no guarantee that input or output to the same file is synchronous when executed in parallel. In this case, the programmer is responsible for synchronizing input and output statements (or routines) using the provided synchronization constructs or library routines. For the case where each thread accesses a different file, no synchronization by the programmer is necessary

2.2. Memory model¶

One of the most relevant features of OmpSs is to handle architectures with disjoint address spaces. By disjoint address spaces we refer to those architectures where the memory of the system is not contained in a single address space. Examples of these architectures would be distributed environments like clusters of SMPs or heterogeneous systems built around accelerators with private memory.

2.2.1. Single address space view¶

OmpSs hides the existence of other address spaces present on the system. Offering the single address space view fits the general OmpSs philosophy of freeing the user from having to explicitly expose the underlying system resources. Consequently, a single OmpSs program can be run on different system configurations without any modification.

In order to correctly support these systems, the programmer has to specify the data that each task will access. Usually this information is the same as the one provided by the data dependencies, but there are cases where there can be extra data needed by the task that is not declared in the dependencies specification (for example because the programmer knows it is a redundant dependence), so OmpSs differentiates between the two mechanisms.

2.2.2. Specifying task data¶

A set of directives allows to specify the data that a task will use. The OmpSs run-time is responsible for guaranteeing that this data will be available to the task code when its execution starts. Each directive also specifies the directionality of the data. The data specification directives are the following:

copy_in(memory-reference-list) The data specified must be available in the address space where the task is finally executed, and this data will be read only.

copy_out(memory-reference-list) The data specified will be generated by the task in the address space where the task will be executed.

copy_inout(memory-reference-list) The data specified must be available in the address space where the task runs, in addition, this data will be be updated with new values.

copy_deps Use the data dependencies clauses (in/out/inout) also as if they were copy_[in/out/inout] clauses.

The syntax accepted on each clause is the same as the one used to declare data dependencies (see Dependence flow section). Each data reference appearing on a task code must either be a local variable or a reference that has been specified inside one of the copy directives. Also, similar to the specification of data dependencies, the data referenced is also limited by the data specified by the parent task, and the access type must respect the access type of the data specified by the parent. The programmer can assume that the implicit task that represents the sequential part of the code has a read and write access to the whole memory, thus, any access specified in a user defined top level task is legal. Failure to respect these restrictions will cause an execution error. Some of these restrictions limit the usage of complex data structures with this mechanism.

The following code shows an OmpSs program that defines two tasks:

float x[128];
float y[128];

int main () {
  for (int i = 0; i < N; i++) {
    #pragma omp target device(smp)
    #pragma omp task inout(x) copy_deps // implicit copy_inout(x)
    do_computation_CPU(x);

    #pragma omp target device(cuda)
    #pragma omp task inout(y) copy_deps // implicit copy_inout(x)
    do_computation_GPU(y);
  }
#pragma omp taskwait
  return 0;
}

One that must be run on a regular CPU, which is marked as target device(smp), and the second which must be run on a CUDA GPU, marked with target device(cuda). This OmpSs program can run on different system configurations, with the only restriction of having at least one GPU available. For example, it can run on a SMP machine with one or more GPUs, or a cluster of SMPs with several GPUs on each node. OmpSs will internally do the required data transfers between any GPU or node of the system to ensure that each tasks receives the required data. Also, there are no references to these disjoint address spaces, data is always referenced using a single address space. This address space is usually referred to as the host address space.

2.2.3. Accessing children task data from the parent task¶

Data accessed by children tasks may not be accessible by the parent task code until a synchronization point is reached. This is so because the status of the data is undefined since the children tasks accessing the data may not have completed the execution and the corresponding internal data transfers. The following code shows an example of this situation:

float y[128];

int main () {
  #pragma omp target device(cuda)
  #pragma omp task copy_inout(y)
  do_computation_GPU(y);

  float value0 = y[64]; // illegal access

  #pragma omp taskwait

  float value1 = y[64]; // legal access

  return 0;
}

The parent task is the implicitly created task and the child task is the single user defined task declared using the task construct. The first assignment (value0 = y[64]) is illegal since the data may be still in use by the child task, the taskwait in the code guarantees that following access to array y is legal.

Synchronization points, besides ensuring that the tasks have completed, also serve to synchronize the data generated by tasks in other address spaces, so modifications will be made visible to parent tasks. However, there may be situations when this behavior is not desired, since the amount of data can be large and updating the host address space with the values computed in other address spaces may be a very expensive operation. To avoid this update, the clause noflush can be used in conjunction with the synchronization taskwait construct. This will instruct OmpSs to create a synchronization point but will not synchronize the data in separate address spaces. The following code illustrates this situation:

float y[128];

int main() {
  #pragma omp target device(cuda)
  #pragma omp task copy_inout(y)
  do_computation_GPU(y);

  #pragma omp taskwait noflush
  float value0 = y[64]; // task has finished, but 'y' may not contain updated data

  #pragma omp taskwait
  float value1 = y[64]; // contains the computed values

  return 0;
}

The assignment value0 = y[64] may not use the results computed by the previous task since the noflush clause instructs the underlying run-time to not trigger data transfers from separate address spaces. The following access (value1 = y[64]) after the taskwait (withouth the noflush clause) will access the updated values.

The taskwait’s dependence clauses (in, out, inout and on) can also be used to synchronize specific pieces of data instead of synchronizing the whole set of currently tracked memory. The following code shows an example of this scenario:

float x[128];
float y[128];

int main () {
  #pragma omp target device(cuda)
  #pragma omp task inout(x) copy_deps // implicit copy_inout(x)
  do_computation_GPU(x);

  #pragma omp target device(cuda)
  #pragma omp task inout(y) copy_deps // implicit copy_inout(y)
  do_computation_GPU(y);

  #pragma omp taskwait on(y)
  float value0 = x[64]; // may be a not updated value
  float value1 = y[64]; // this value has been updated

  ...
}

The value read by the definition of value0 corresponds to the value already computed by one of the previous generated tasks (i.e. the one annotated with inout(y) copy_deps). However, the value read by the definition of value1 may not corresponds with the updated value of x. The taskwait in this code only synchronizes data referenced in the clause on (i.e. the array y).

2.4. Asynchronous execution¶

The most notable difference from OmpSs to OpenMP is the absence of the parallel clause in order to specify where a parallel region starts and ends. This clause is required in OpenMP because it uses a fork-join execution model where the user must specify when parallelism starts and ends. OmpSs uses the model implemented by StarSs where parallelism is implicitly created when the application starts. Parallel resources can be seen as a pool of threads–hence the name, thread-pool execution model–that the underlying run-time will use during the execution. The user has no control over this pool of threads, so the standard OpenMP methods omp_get_num_threads() or its variants are not available to use.

OmpSs allows the expression of parallelism through tasks. Tasks are independent pieces of code that can be executed by the parallel resources at run-time. Whenever the program flow reaches a section of code that has been declared as task, instead of executing the task code, the program will create an instance of the task and will delegate the execution of it to the OmpSs run-time environment. The OmpSs run-time will eventually execute the task on a parallel resource.

Another way to express parallelism in OmpSs is using the clause for. This clause has a direct counterpart in OpenMP and in OmpSs has an almost identical behavior. It must be used in conjunction with a for loop (in C or C++) and it encapsulates the iterations of the given for loop into tasks, the number of tasks created is determined by the OmpSs run-time, however the user can specify the desired scheduling with the clause schedule.

Any directive that defines a task or a series of tasks can also appear within a task definition. This allows the definition of multiple levels of parallelism. Defining multiple levels of parallelism can lead to a better performance of applications, since the underlying OmpSs run-time environment can exploit factors like data or temporal locality between tasks. Supporting multi-level parallelism is also required to allow the implementation of recursive algorithms.

Synchronizing the parallel tasks of the application is required in order to produce a correct execution, since usually some tasks depend on data computed by other tasks. The OmpSs programming model offers two ways of expressing this: data dependencies, and explicit directives to set synchronization points.

2.5. Dependence flow¶

Asynchronous parallelism is enabled in OmpSs by the use data-dependencies between the different tasks of the program. OmpSs tasks commonly require data in order to do meaningful computation. Usually a task will use some input data to perform some operations and produce new results that can be later on be used by other tasks or parts of the program.

When an OmpSs programs is being executed, the underlying runtime environment uses the data dependence information and the creation order of each task to perform dependence analysis. This analysis produces execution-order constraints between the different tasks which results in a correct order of execution for the application. We call these constraints task dependences.

Each time a new task is created its dependencies are matched against of those of existing tasks. If a dependency, either Read-after-Write (RaW), Write-after-Write (WaW) or Write-after-Read(WaR), is found the task becomes a successor of the corresponding tasks. This process creates a task dependency graph at runtime. Tasks are scheduled for execution as soon as all their predecessor in the graph have finished (which does not mean they are executed immediately) or at creation if they have no predecessors.

The OpenMP task construct is extended with the in (standing for input), out (standing for output), inout (standing for input/output), concurrent and commutative clauses to this end. They allow to specify for each task in the program what data a task is waiting for and signaling is readiness. Note that whether the task really uses that data in the specified way its the programmer responsibility. The meaning of each clause is explained below:

in(memory-reference-list): If a task has an in clause that evaluates to a given lvalue, then the task will not be eligible to run as long as a previously created sibling task with an out, inout, concurrent or commutative clause applying to the same lvalue has not finished its execution.

out(memory-reference-list): If a task has an out clause that evaluates to a given lvalue, then the task will not be eligible to run as long as a previously created sibling task with an in, out, inout concurrent or commutative clause applying to the same lvalue has not finished its execution.

inout(memory-reference-list): If a task has an inout clause that evaluates to a given lvalue, then it is considered as if it had appeared in an in clause and in an out clause. Thus, the semantics for the in and out clauses apply.

concurrent(memory-reference-list): the concurrent clause is a special version of the inout clause where the dependencies are computed with respect to in, out, inout and commutative but not with respect to other concurrent clauses. As it relaxes the synchronization between tasks users must ensure that either tasks can be executed concurrently either additional synchronization is used.

commutative(memory-reference-list): If a task has a commutative clause that evaluates to a given lvalue, then the task will not become a member of the commutative task set for that lvalue as long as a previously created sibling task with an in, out, inout or concurrent clause applying to the same lvalue has not finished its execution. Given a non-empty commutative task set for a certain lvalue, any task of that set may be eligible to run, but just one at the same time. Thus, tasks that are members of the same commutative task set are executed keeping mutual exclusion among them.

All of these clauses receive a list of memory references as argument. The syntax permitted to specify memory references is described in Language section. The data references provided by these clauses are commonly named the data dependencies of the task.

Note

For compatibility with earlier versions of OmpSs, you can use clauses input and output with exactly the same semantics of clauses in and out respectively.

The following example shows how to define tasks with task dependences:

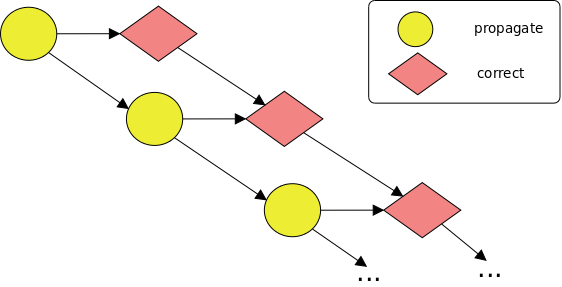
void foo (int *a, int *b) {
  for (int i = 1; i < N; i++) {
#pragma omp task in(a[i-1]) inout(a[i]) out(b[i])
      propagate(&a[i-1], &a[i], &b[i]);

#pragma omp task in(b[i-1]) inout(b[i])
       correct(&b[i-1], &b[i]);
  }
}

This code generates at runtime the following task graph:

The following example shows how we can use the concurrent clause to parallelize a reduction over an array:

#include<stdio.h>
#define N 100

void reduce(int n, int *a, int *sum) {
  for (int i = 0; i < n; i++) {
#pragma omp task concurrent(*sum)
    {
#pragma omp atomic
      *sum += a[i];
    }
  }
}

int main() {
  int i, a[N];
  for (i = 0; i < N; ++i)
      a[i] = i + 1;

  int sum = 0;
  reduce(N, a, &sum);

#pragma omp task in(sum)
printf("The sum of all elements of 'a' is: %d\n", sum);

#pragma omp taskwait
  return 0;
}

Note that all tasks that compute the sum of the values of ‘a’ may be executed concurrently. For this reason we have to protect with an atomic construct the access to the ‘sum’ variable. As soon as all of these tasks finish their execution, the task that prints the value of ‘sum’ may be executed.

Note that the previous example can also be implemented using the commutative clause (we only show the reduce function, the rest of the code is exactly the same):

void reduce(int n, int *a, int *sum) {
  for (int i = 0; i < n; i++) {
#pragma omp task commutative(*sum)
      *sum += a[i];
  }
}

Note that using the commutative clause only one task of the commutative task set may be executed at the same time. Thus, we don’t need to add any synchronization when we access to the ‘sum’ variable.

2.5.1. Extended lvalues¶

All dependence clauses allow extended lvalues from those of C/C++. Two different extensions are allowed:

Array sections allow to refer to multiple elements of an array (or pointed data) in single expression. There are two forms of array sections:

a[lower : upper]. In this case all elements of ‘a’ in the range of lower to upper (both included) are referenced. If no lower is specified it is assumed to be 0. If the array section is applied to an array and upper is omitted then it is assumed to be the last element of that dimension of the array.

a[lower; size]. In this case all elements of ‘a’ in the range of lower to lower+(size-1) (both included) are referenced.

Shaping expressions allow to recast pointers into array types to recover the size of dimensions that could have been lost across function calls. A shaping expression is one or more [size] expressions before a pointer.

The following example shows examples of these extended expressions:

void sort(int n, int *a) {
  if (n < small) seq_sort(n, a);

#pragma omp task inout(a[0:(n/2)-1]) // equivalent to inout(a[0;n/2])
       sort(n/2, a);
#pragma omp task inout(a[n/2:n-1]) // equivalent to inout(a[n/2;n-(n/2)])
       sort(n/2, &a[n/2]);
#pragma omp task inout(a[0:(n/2)-1], a[n/2:n-1])
       merge (n/2, a, a, &a[n/2]);
#pragma omp taskwait
}

Note

Our current implementation only supports array sections that completely overlap. Implementation support for partially overlapped sections is under development.

Note that these extensions are only for C/C++, since Fortran supports, natively, array sections. Fortran array sections are supported on any dependence clause as well.

2.5.2. Dependences on the taskwait construct¶

In addition to the dependencies mechanism, there is a way to set synchronization points in an OmpSs application. These points are defined using the taskwait directive. When the control flow reaches a synchronization point, it waits until all previously created sibling tasks complete their execution.

OmpSs also offers synchronization point that can wait until certain tasks are completed. These synchronization points are defined adding any kind of task dependence clause to the taskwait construct.

In the following example we have two tasks whose execution is serialized via dependences: the first one produces the value of x whereas the second one consumes x and produces the value of y. In addition to this, we have a taskwait construct annotated with an input dependence over x, which enforces that the execution of the region is suspended until the first task complete execution. Note that this construct does not introduce any restriction on the execution of the second task:

int main() {
  int x = 0, y = 2;

  #pragma omp task inout(x)
  x++;

  #pragma omp task in(x) inout(y)
  y -= x;

  #pragma omp taskwait in(x)
  assert(x == 1);

  // Note that the second task may not be executed at this point

  #pragma omp taskwait
  assert(x == y);
}

Note

For compatibility purposes we also support the on clause on the taskwait construct, which is an alias of inout.

2.5.3. Multidependences¶

Multidependences is a powerful feature that allow us to define a dynamic number of any kind of dependences. From a theoretical point of view, a multidependence consists on two different parts: first, an lvalue expression that contains some references to an identifier (the iterator) that doesn’t exist in the program and second, the definition of that identifier and its range of values. Depending on the base language the syntax is a bit different:

dependence-type({memory-reference-list, iterator-name = lower; size}) for C/C++.

dependence-type([memory-reference-list, iterator-name = lower, size]) for Fortran.

Despite having different syntax for C/C++ and Fortran, the semantics of this feature is the same for the 3 languages: the lvalue expression will be duplicated as many times as values the iterator have and all the references to the iterator will be replaced by its values.

The folllowing code shows how to define a multidependence in C/C++:

void foo(int n, int *v)
{
// This dependence is equivalent to inout(v[0], v[1], ..., v[n-1])
#pragma omp task inout({v[i], i=0;n})
    {
        int j;
        for (int j = 0; j < n; ++j)
            v[j]++;
    }
}

And a similar code in Fortran:

subroutine foo(n, v)
    implicit none
    integer :: n
    integer :: v(n)

    ! This dependence is equivalent to inout(v[1], v[2], ..., v[n])
    !$omp task inout([v(i), i=1, n])
        v = v + 1
    !$omp end task
end subroutine foo

Warning

Multidependences syntax may change in a future

2.6. Task scheduling¶

When the current executed task reaches a task scheduling point, the implementation may decide to switch from this task to another one from the set of eligible tasks. Task scheduling points may occur at the following locations:

in a task generating code

in a taskyield directive

in a taskwait directive

just after the completion of a task

The fact of switching from a task to a different one is known as task switching and it may imply to begin the execution of a non-previously executed task or resumes the execution of a partially executed task. Task switching is restricted in the following situations:

the set of eligible tasks (at a given time) is initially formed by the set of tasks included in the ready task pool (at this time).

once a tied task has been executed by a given thread, it can be only resumed by the very same thread (i.e. the set of eligible tasks for a thread does not include tied tasks that has been previously executed by a different thread).

when creating a task with the if clause for which expression evaluated to false, the runtime must offer a mechanism to immediately execute this task (usually by the same thread that creates it).

when executing in a final context all the encountered task generating codes will execute the task immediately after creating it as if it was a simple routine call (i.e. the set of eligible tasks in this situation is restricted to include only the newly generated task).

Note

Remember that the ready task pool does not include tasks with dependences still not fulfilled (i.e. not all its predecessors have finished yet) or blocked tasks in any other condition (e.g. tasks executing a taskwait with non-finished child tasks).

2.7. Task reductions¶

The reduction clause allow us to define an asynchronous task reduction over a list of items. For each item, a private copy is created for each thread that participates in the reduction. At task synchronization (dependence or taskwait), the original list item is updated with the values of the private copies by applying the combiner associated with the reduction-identifier. Consequently, the scope of a reduction begins when the first reduction task is created and ends at a task synchronization point. This region is called the reduction domain.

The taskwait construct specifies a wait on the completion of child tasks in the context of the current task and combines all privately allocated list items of all child tasks associated with the current reduction domain. A taskwait therefore represents the end of a domain scope.

The following example computes the sum of all values of the nodes of a linked-list. The final result of the reduction is computed at the taskwait:

struct node_t {
  int val;
  struct node_t* next;
};

int sum_values(struct node_t* node) {
  int red=0;
  struct node_t* current = node;

  while (current != 0) {
#pragma omp task reduction(+: red)
    {
      red += current->val;
    }
    node = node->next;
  }
#pragma omp taskwait

  return red;
}

Data-flow based task execution allows a streamline work scheduling that in certain cases results in higher hardware utilization with relatively small development effort. Task-parallel reductions can be easily integrated into this execution model but require the following assumption. A list item declared in the task reduction directive is considered as if declared concurrent by the depend clause.

In the following code we can see an example where a reduction domain begins with the first occurrence of a participating task and is implicitly ended by a dependency of a successor task.:

#include<assert.h>

int main(int argc, char *argv[]) {

  const int SIZE  = 1024;
  const int BLOCK =   32;
  int array[SIZE];

  int i;

  for (i = 0; i < SIZE; ++i)
    array[i] = i+1;

  int red = 0;
  for (int i = 0; i < SIZE; i += BLOCK) {
#pragma omp task shared(array) reduction(+:red)
    {
      for (int j = i; j < i+BLOCK; ++j)
        red += array[j];
    }
  }
#pragma omp task in(red)
    assert(red == ((SIZE * (SIZE+1))/2));

#pragma omp taskwait
}

Nested task constructs typically occur in two cases. In the first, each task at each nesting level declares a reduction over the same variable. This is called multilevel reduction. It is important to point out that only task synchronization that occurs at the same nesting level at which a reduction scope was created (that is the nesting level that first encounter a reduction task for a list item), ends the scope and reduces private copies. Within the reduction domain, the value of the reduction variable is unspecified.

In the second occurrence each nesting level reduces over a different reduction variable. This happens for example if a nested task performs a reduction on task local data. In this case a taskwait at the end of each nesting level is required. We call this occurrence a nested-domain reduction.

2.8. Runtime Library Routines¶

OmpSs uses runtime library routines to set and/or check the current execution environment, locks and timing services. These routines are implementation defined and you can find a list of them in the correspondant runtime library user guide.

2.9. Environment Variables¶

OmpSs uses environment variables to configure certain aspects of its execution. The set of these variables is implementation defined and you can find a list of them in the correspondant runtime library user guide.

2. Programming model¶

2.1. Execution model¶

2.2. Memory model¶

2.2.1. Single address space view¶

2.2.2. Specifying task data¶

2.2.3. Accessing children task data from the parent task¶

2.3. Data sharing rules¶

2.4. Asynchronous execution¶

2.5. Dependence flow¶

2.5.1. Extended lvalues¶

2.5.2. Dependences on the taskwait construct¶

2.5.3. Multidependences¶

2.6. Task scheduling¶

2.7. Task reductions¶

2.8. Runtime Library Routines¶

2.9. Environment Variables¶