Dependence model¶
Asynchronous parallelism is enabled in OmpSs-2 by the use of data-dependencies between the different tasks of the program. OmpSs-2 tasks commonly require data in order to do meaningful computation. Usually a task will use some input data to perform some operations and produce new results that can be later used by other tasks or parts of the program.
When an OmpSs-2 program is being executed, the underlying run-time system uses the data dependence information and the creation order of each task to perform dependence analysis. This analysis produces execution-order constraints between the different tasks which results in a correct order of execution for the application. We call these constraints task dependences.
Each time a new task is created its dependencies are matched against those of existing tasks. If a dependency, either Read-after-Write (RaW), Write-after-Write (WaW) or Write-after-Read(WaR), is found the task becomes a successor of the corresponding tasks. This process creates a task dependency graph at run-time. Tasks are scheduled for execution as soon as all their predecessors in the graph have finished (which does not mean they are executed immediately) or at creation if they have no predecessors.
In the general case, the statement that follows the pragma is to be executed asynchronously. Whenever a thread encounters a task construct, it instantiates the task and resumes its execution after the construct. The task instance can be executed either by that same thread at some other time or by another thread. The semantics can be altered through additional clauses and through the properties of the enclosing environment in which the task is instantiated.
Dependencies allow tasks to be scheduled after other tasks using the depend clause. They allow to specify for each task in the program what data a task is waiting for and signaling is readiness. Note that whether the task uses that data in the specified way is the responsibility of the programmer.
The depend clause admits the following keywords: in, out, inout, concurrent or commutative.
The keyword is followed by a colon and a comma-separated list of elements (memory references).
The syntax permitted to specify memory references is described in Language section.
The data references provided by these clauses are commonly named the data dependencies of the task.
The semantics of the depend clause are also extended with the in (standing for input), out (standing for output), inout (standing for input/output), concurrent and commutative clauses to this end.
All these clauses also admit a comma-separated list of elements (memory references) as described in the previous paragraph.
The meaning of each clause/keyword is explained below:
in(memory-reference-list): If a task has aninclause that evaluates to a given lvalue, then the task will not be eligible to run as long as a previously created sibling task with anout,inout,concurrentorcommutativeclause applying to the same lvalue has not finished its execution.out(memory-reference-list): If a task has anoutclause that evaluates to a given lvalue, then the task will not be eligible to run as long as a previously created sibling task with anin,out,inout,concurrentorcommutativeclause applying to the same lvalue has not finished its execution.inout(memory-reference-list): If a task has aninoutclause that evaluates to a given lvalue, then it is considered as if it had appeared in aninclause and in anoutclause. Thus, the semantics for theinandoutclauses apply.concurrent(memory-reference-list): Theconcurrentclause is a special version of theinoutclause where the dependencies are computed with respect toin,out,inoutandcommutativebut not with respect to other concurrent clauses. As it relaxes the synchronization between tasks users must ensure that either tasks can be executed concurrently or additional synchronization is used.commutative(memory-reference-list): If a task has a commutative clause that evaluates to a given lvalue, then the task will not become a member of the commutative task set for that lvalue as long as a previously created sibling task with anin,out,inoutorconcurrentclause applying to the same lvalue has not finished its execution. Given a non-empty commutative task set for a certain lvalue, any task of that set may be eligible to run, but just one at the same time. Thus, tasks that are members of the same commutative task set are executed keeping mutual exclusion among them.
The usual scope of the dependency calculation is restricted to that determined by the enclosing (possibly implicit) task. That is, the contents of the depend clause of two tasks can determine dependencies between them only if they share the same parent task. In this sense, tasks define an inner dependency domain into which to calculate the dependencies between its direct children. However, OmpSs-2 improves the combination of data dependencies and task nesting, as will be explained in the next sections.
The following example shows how to define tasks with task dependences:
void foo (int *a, int *b) {
for (int i = 1; i < N; i++) {
#pragma oss task in(a[i-1]) inout(a[i]) out(b[i])
propagate(&a[i-1], &a[i], &b[i]);
#pragma oss task in(b[i-1]) inout(b[i])
correct(&b[i-1], &b[i]);
}
}
This code generates at run-time the following task graph:
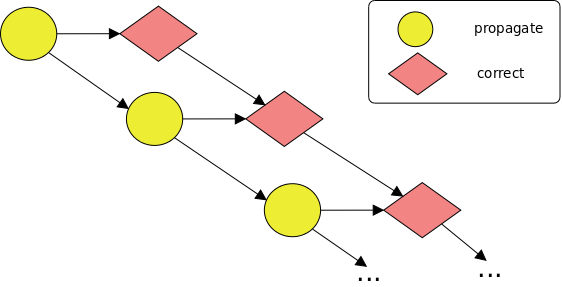
The following example shows how we can use the concurrent clause to parallelize a reduction over an array:
#include <stdio.h>
#define N 100
void reduce(int n, int *a, int *sum) {
for (int i = 0; i < n; i++) {
#pragma oss task concurrent(*sum)
{
#pragma oss atomic
*sum += a[i];
}
}
}
int main() {
int i, a[N];
for (i = 0; i < N; ++i)
a[i] = i + 1;
int sum = 0;
reduce(N, a, &sum);
#pragma oss task in(sum)
printf("The sum of all elements of 'a' is: %d\n", sum);
#pragma oss taskwait
return 0;
}
Note that all tasks that compute the sum of the values of a may be executed concurrently.
For this reason we have to protect with an atomic construct the access to the sum variable.
As soon as all of these tasks finish their execution, the task that prints the value of sum may be executed.
The following example shows how we can use the commutative clause:
#include <stdio.h>
int main() {
int a;
#pragma oss task out(a) // Task T1
a = 10;
#pragma oss task commutative(a) // Task T2
printf("Intermediate alue of 'a': %d\n", a++);
#pragma oss task commutative(a) // Task T3
printf("Intermediate value of 'a': %d\n", a++);
#pragma oss task in(a) // Task T4
printf("Final value of 'a' is: %d\n", a);
#pragma oss taskwait
return 0;
}
Note that the commutative tasks (T2 and T3) will be executed after the task that initializes a (T1), and before the task that prints the final value of a (T4).
No execution order of the commutative tasks is not guaranteed but they will not be executed at the same time by definition.
Thus, it is safe to modify the value of a inside those tasks.
Combining task nesting and dependencies¶
Being able to combine task nesting and dependences is important for programmability. The code below shows an example that combines nesting and dependencies with two levels of tasks. For brevity, the inner tasks do not have dependencies between their siblings.
#pragma oss task inout(a, b) // Task T1
{
a++; b++;
#pragma oss task inout(a) // Task T1.1
a += ...;
#pragma oss task inout(b) // Task T1.2
b += ...;
}
#pragma oss task in(a, b) out(z, c, d) // Task T2
{
z = ...;
#pragma oss task in(a) out(c) // Task T2.1
c = ... + a + ...;
#pragma oss task in(b) out(d) // Task T2.2
d = ... + b + ...;
}
#pragma oss task in(a, b, d) out(e, f) // Task T3
{
#pragma oss task in(a, d) out(e) // Task T3.1
e = ... + a + d + ...;
#pragma oss task in(b) out(f) // Task T3.2
f = ... + b + ...;
}
#pragma oss task in(c, d, e, f) // Task T4
{
#pragma oss task in(c, e) // Task T4.1
... = ... + c + e + ...;
#pragma oss task in(d, f) // Task T4.2
... = ... + d + f + ...;
}
#pragma oss taskwait
To parallelize the original code using a top-down approach we would perform the following steps.
First, we would add the pragmas of the outer tasks.
Since they have conflicting accesses over some variables, we add the corresponding dependency clauses (e.g., in and out) for each of their accessed variables.
In general, it is a good practice to have entries to protect all the accesses of a task.
Doing this reduces the burden on the programmer, improves the maintainability of the code and reduces the chances of overlooking conflicting accesses.
Then, inside each task, we identify separate functionalities and convert each into a task. If we follow the same approach, the depend clause of each inner task will contain entries to protect its own accesses.
When we consider how the depend clauses are composed, we observe that outer tasks contain a combination of elements to protect their own accesses and elements that are only needed by their subtasks. This is necessary to avoid data-races between subtasks with different parents. Note that parent tasks do not execute a taskwait at the end of their task body. Unlike OpenMP and OmpSs, OmpSs-2 automatically links the dependency domain of a task with that of its subtasks. Once a task finishes its execution, the dependencies that are not included in any of its unfinished subtasks are released. In contrast, the release of the dependencies that appear in any of its unfinished subtasks is delayed until these latter finish.
We strongly recommend avoiding taskwaits at the end of task bodies. Not only do they delay the finalization of tasks, but also hinder the discovery of parallelism. Moreover, taskwait delays the release of all dependencies until all subtasks finish, even the dependencies not declared by any subtask. Nevertheless, it is worth noting that the variables stored in the stack of the parent task are no longer valid once it returns from its task body. In the next section, we explain in detail the benefits of automatically linking dependency domains across task nesting levels without taskwaits.
Fine-grained release of dependencies across nesting levels¶
Detaching the taskwait at the end of a task from the task code allows the run-time system to be made aware earlier of the fact that the task code has finished and that it will not create further subtasks. In a scenario with task nesting and dependencies, this knowledge allows it to make assumptions about dependencies. Since the task code is finished, the task will no longer any action that may require the enforcement of its dependencies by itself. Only the dependencies needed by its live subtasks need to be preserved. In most cases, these dependencies are the ones associated with an element of the depend clause that also appears in a live subtask. Therefore, the dependencies that do not need to be enforced anymore could be released.
This incremental fine-grained release of dependencies is the default behaviour in OmpSs-2 tasks.
However, this behaviour can be disabled with the wait clause, which defers the release of all dependencies of a task until it has finished the execution of its body and all its subtasks deeply complete.
This clause emulates a taskwait-like operation immediately after exiting from the task code, but avoids the overhead and drawbacks of a taskwait.
Notice that this improvement is only possible once the run-time system is aware of the end of the code of a task.
However, it may also be desirable to trigger this mechanism earlier.
For instance, a task may use certain data only at the beginning and then perform other lengthy operations that delay the release of the dependencies associated with that data.
The release directive asserts that a task will no longer perform accesses that conflict with the contents of the associated depend clause.
The contents of the depend clause must be a subset of that of the task construct that is no longer referenced in the rest of the lifetime of the task and its future subtasks.
Weak dependences¶
Some of the elements of the depend clause may be needed by the task itself, others may be needed only by its subtasks, and others may be needed by both. The ones that are only needed for the subtasks only serve as a mechanism to link the outer domain of dependencies to the inner one. In this sense, allowing them to defer the execution of the task is unnecessary, since the task does not perform any conflicting accesses by itself.
The dependence model in OmpSs-2 has been extended to define the weak counterparts of in, out, inout and commutative dependences.
Their semantics are analogous to the ones without the weak prefix.
However, the weak variants indicate that the task does not perform by itself any action that requires the enforcement of the dependency.
Instead those actions can be performed by any of its deeply nested subtasks.
Any subtask that may directly perform those actions needs to include the element in its depend clause in the non-weak variant.
In turn, if the subtask delegates the action to a subtask, the element must appear in its depend clause using at least the weak variant.
Weak variants do not imply a direct dependency, and thus do not defer the execution of tasks. Their purpose is to serve as a linking point between the dependency domains of each nesting level. Until now, out of all the tasks with the same parent, the first one with a given element in its depends clause was assumed to not have any input dependency. However, this assumption is no longer true since the dependency domains are no longer isolated. Instead, if the parent has that same element with a weak dependency type, there may be a previous and unfinished task with a depend clause that has a dependency to it. If we calculated dependencies as if all types were non-weak, in such a case, the source of the dependency, if any, would be the source of the non-enforced dependency on its parent over the same element.
This change, combined with the fine-grained release of dependencies, merges the inner dependency domain of a task into that of its parent. Since this happens at every nesting level, the result is equivalent to an execution in which all tasks had been created in a single dependency domain.
Extended data dependencies expressions¶
All dependence clauses allow extended lvalues from those of C/C++. Two different extensions are allowed:
Array sections allow to refer to multiple elements of an array (or pointed data) in a single expression. There are two forms of array sections:
a[lower : upper]. In this case all elements of ‘a’ in the range of lower to upper (both included) are referenced. If no lower is specified it is assumed to be 0. If the array section is applied to an array and upper is omitted then it is assumed to be the last element of that dimension of the array.
a[lower; size]. In this case all elements of ‘a’ in the range of lower to lower+(size-1) (both included) are referenced.Shaping expressions allow to recast pointers into array types to recover the size of dimensions that could have been lost across function calls. A shaping expression is one or more
[size]expressions before a pointer.
Implementations may choose not to support the extended data dependencies model, in which case array sections and shaping expressions will register a single dependency to the first element of the specified range. For example, an expression of the form a[lower : upper] will be interpreted as a dependency over a[lower].
The following example shows examples of these extended expressions:
void sort(int n, int *a) {
if (n < small) seq_sort(n, a);
#pragma oss task inout(a[0:(n/2)-1]) // equivalent to inout(a[0;n/2])
sort(n/2, a);
#pragma oss task inout(a[n/2:n-1]) // equivalent to inout(a[n/2;n-(n/2)])
sort(n/2, &a[n/2]);
#pragma oss task inout(a[0:(n/2)-1], a[n/2:n-1])
merge (n/2, a, a, &a[n/2]);
#pragma oss taskwait
}
Note that these extensions are only for C/C++, since Fortran supports, natively, array sections. Fortran array sections are supported on any dependence clause as well.
Dependences on the taskwait construct¶
In addition to the dependencies mechanism, there is a way to set synchronization points in an OmpSs-2 application.
These points are defined using the taskwait directive.
When the control flow reaches a synchronization point, it waits until all previously created sibling tasks deeply complete.
OmpSs-2 also offers synchronization points that can wait until certain tasks are completed.
These synchronization points are defined by adding any kind of task dependence clause to the taskwait construct.
Multidependences¶
Multidependences is a powerful feature that allows defining a dynamic number of any kind of dependences. From a theoretical point of view, a multidependence consists of two different parts: first, an lvalue expression that contains some references to an identifier (the iterator) that doesn’t exist in the program and second, the definition of that identifier and its range of values. Depending on the base language the syntax is a bit different:
dependence-type({memory-reference-list, iterator-name = lower; size})for C/C++.
dependence-type([memory-reference-list, iterator-name = lower, size])for Fortran.
Additionally, a multidependence may specify the step of the range in the following way:
dependence-type({memory-reference-list, iterator-name = lower; size : step})for C/C++.
dependence-type([memory-reference-list, iterator-name = lower, size, step])for Fortran.
Despite having different syntax for C/C++ and Fortran, the semantics of this feature is the same for the 3 languages: the lvalue expression will be duplicated as many times as values the iterator have and all the references to the iterator will be replaced by its values.
The following code shows how to define a multidependence in C/C++:
void foo(int n, int *v)
{
// This dependence is equivalent to inout(v[0], v[1], ..., v[n-1])
#pragma oss task inout({v[i], i=0;n})
{
for (int j = 0; j < n; ++j)
v[j]++;
}
}
And a similar code in Fortran:
subroutine foo(n, v)
implicit none
integer :: n
integer :: v(n)
! This dependence is equivalent to inout(v[1], v[2], ..., v[n])
!$oss task inout([v(i), i=1, n])
v = v + 1
!$oss end task
end subroutine foo